De formule van Camp: de sleutel tot optimaal voorraadbeheer

Om voorraadproblemen te voorkomen, wordt de formule van Camp of EOQ (Economic Order Quantity) gebruikt als wiskundige methode om te berekenen hoe vaak en in welke hoeveelheid een bestelling bij een leverancier moet worden geplaatst, zodat een goed voorraadbeheer gewaarborgd is.

Dit model wordt vaak geassocieerd met de aankoop van grondstoffen en een optimaal voorraadbeheer, maar eigenlijk kan de formule van Camp worden toegepast op elk type grondstof.

Formule van Camp of Wilson

Een andere formule is die van de Amerikaanse ingenieur Ford Whitman Harris uit 1913. Het duurde echter uiteindelijk tot 1934 voordat consultant R.H. Wilson die formule met succes ontwikkelde voor gebruik in de praktijk. Hoe worden de berekeningen gemaakt?

Door te kijken naar de vraag naar een product, de kosten voor het plaatsen van een bestelling en de opslagkosten kan je het optimale bestelvolume bepalen. De wiskundige formule is als volgt:

• Q = optimale bestelhoeveelheid
• D = jaarlijkse vraag naar de betrokken grondstof
• K = kosten per bestelling
• G = kosten voor de opslag van een eenheid in het magazijn gedurende een bepaalde tijd

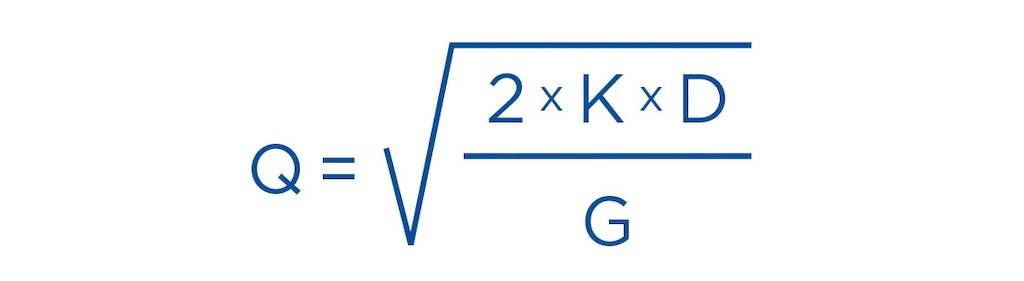
Toepassingen en beperkingen

Het doel van dit wiskundige model is het inkoopvolume van een bepaald product te optimaliseren door te bepalen wanneer een bestelling bij een leverancier moet worden geplaatst en in welke hoeveelheid.

Met deze informatie kunnen we ook het bestelpunt bepalen (wanneer elke bestelling moet worden geplaatst), rekening houdend met de doorlooptijd en de veiligheidsvoorraad. De methode van Wilson heeft echter bepaalde beperkingen. Deze wiskundige oplossing is alleen van toepassing op ondernemingen die aan de volgende twee hypotheses voldoen:

• De onderneming heeft het hele jaar door een constante vraag naar grondstoffen
• De kostprijs van het product blijft stabiel, zonder grote prijsschommelingen in de loop van het jaar.

Bijvoorbeeld, als de kosten van de grondstoffen variëren naar gelang van het seizoen, gaat deze wiskundige formule niet langer op, omdat er geen rekening wordt gehouden met deze variabele.

Bijgevolg is deze methode enkel geschikt voor bepaalde ondernemingen waar de vraag en de kosten vrij stabiel blijven in de loop van het jaar.

Voordelen van deze methode

Voor bedrijven die aan beide voorwaarden voldoen, garandeert deze wiskundige methode een optimalisering van het voorraadbeheer. Deze oplossing heeft namelijk de volgende voordelen:

• De aankoop- en opslagkosten worden tot een minimum beperkt.
• Voorraadoverschotten worden vermeden, terwijl er te allen tijde voldoende voorraad is om aan de vraag te voldoen.
• We weten precies hoeveel stuks we moeten bestellen.
• Voorraadtekorten worden vermeden.

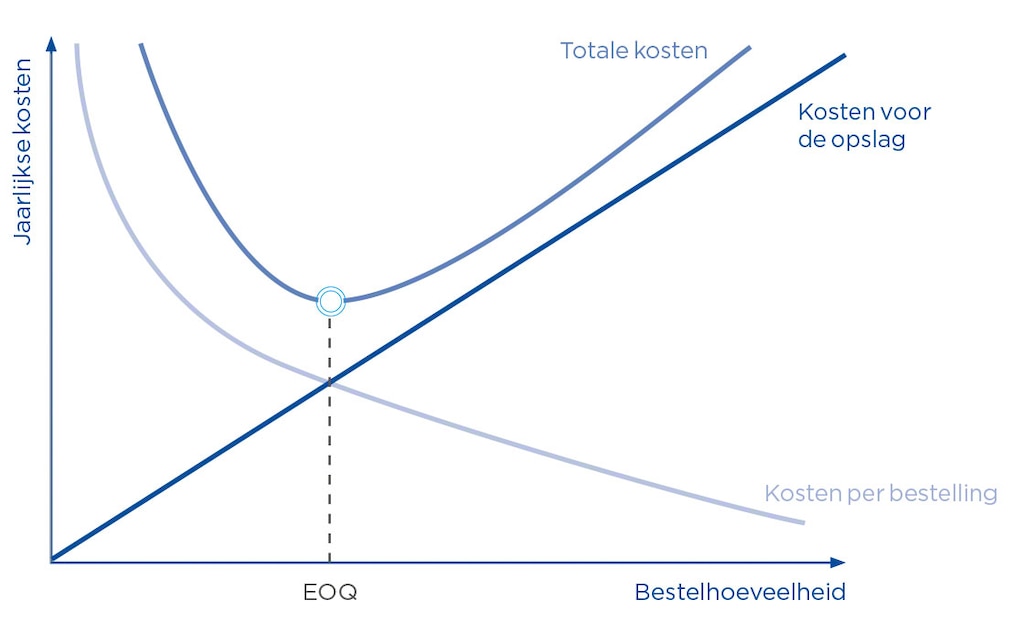
Praktische toepassing van de formule van Camp

Het fictieve bedrijf Orch Kork produceert en verdeelt fleskurken voor lokale wijnbouwbedrijven. Om de jaarlijkse productie van 10.000 stuks te halen, koopt het bedrijf het hele jaar door 1.000 kg kurkeikenschors.

Gesteld dat elke bestelling 200 euro kost (inclusief transportkosten) en de opslagkosten niet meer dan 2.000 euro per jaar bedragen, wat is dan het optimale bestelvolume?

In dit geval zou Q (de optimale bestelhoeveelheid) worden bepaald door de vierkantswortel van de volgende formule (2*200*1000/2000). Het resultaat is dan 14,14.

Orch Kork zal dus telkens 14 kg moeten bestellen om over een optimale hoeveelheid kilo's kurkeikenschors te beschikken voor hun productie, zodat zowel opslagoverschotten als mogelijke stockbreuken worden vermeden. Het bedrijf moet dus 71 bestellingen per jaar van telkens 14 kg moeten plaatsen om aan 1000 kg kurkeikenschors te komen.

EOQ: voorraadkosten minimaliseren als er geen seizoensgebonden pieken of dalen zijn

Uiteindelijk zal het bedrijf het bestelproces kunnen optimaliseren en zo de totale opslag- en inkoopkosten minimaliseren door gebruik te maken van de formule van Camp. Dit model is echter enkel van toepassing wanneer de vraag en de prijzen het hele jaar door constant zijn. Voor complexere situaties is het model nutteloos en in dat geval zullen we moeten vertrouwen op een Warehouse Management Systeem.